Riporto un mio positivo esperimento di pratico bilanciamento del telescopio Dobson, con l’uso di molle di trazione in sostituzione di pesanti contrappesi.
Un telescopio Dobson si comporta in pratica come una leva di primo genere, cioè come una bilancia classica a due bracci e fulcro centrale: Il braccio, diciamo A (vedi figura); va dalla cella dello specchio primario al fulcro della leva coincidente col centro dei cuscinetti ” a mezzaluna” di altitudine; e il braccio, diciamo B, che va da questo centro fino all’estremo alto opposto, costituito dal traliccio di tubi che termina con la cassa dello specchio secondario.
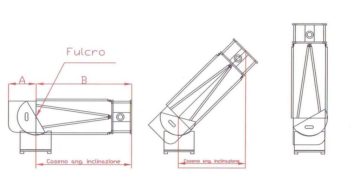
La forza di bilanciamento richiesta, aumenta con il Coseno dell’angolo di inclinazione del telescopio, ed è zero col telescopio che punta allo zenit
E’ questa in pratica la leva di primo genere che ha il fulcro posto fra i due estremi opposti che rappresentano la potenza e la resistenza, i quali devono essere bilanciati per conseguire un desiderato reciproco equilibrio, che permetta al telescopio di non muoversi dalla posizione in cui viene puntato.
La precisione dell’equilibrio cercato non è in genere critica, in quanto esiste, per i telescopi ben fatti, la tolleranza di fondo, sempre fornita dall’attrito dell’accoppiamento dei cuscinetti di altitudine fatto con materiali tipo teflon–Fòrmica “ebony star”… (o teflon ed altri laminati “HPL” alias la Fòrmica versione italiana con la necessaria superficie “sabbiosa” tipo la ABET LAMINATI print HPL “decori minimi n° 236” o 563 di catalogo, e consimili).
La recente escalation dei progetti verso dobson sempre più leggeri per aumentarne la facilità di trasporto, comporta la progressiva difficoltà del loro bilanciamento, in quanto, per alleggerire si privilegia una cassa del primario molto bassa, quindi con il braccio della leva A molto corto, che rischia di determinare un momento resistente non più in grado di bilanciare il momento potente del lato B opposto della bilancia, che notoriamente è dato dal momento complessivo generato dalla somma dei momenti di ogni componente presente sul lato B della leva. Per esempio: traliccio + cassa del secondario + specchio secondario e suo supporto + focheggiatore + oculare + cercatore ottico + cercatore tipo Red-dot oppure Telrad.
Oggi, a non favorire il bilanciamento concorrono pure gli oculari a grande campo, spettacolari, comodi e molto performanti… ma molto più pesanti dei vecchi oculari.
Per una leva meccanica come il telescopio dobson vale sempre la regola che per bilanciare il peso di un oculare da un ettogrammo inserito al focheggiatore di un telescopio con rapporto focale (ad esempio) F=5, occorre aggiungere “F volte”, cioè mezzo chilogrammo di peso dietro allo specchio primario.
(In ottica, quella lettera F rappresenta il rapporto fra la lunghezza focale dell’obiettivo, divisa per il suo diametro. Ad esempio, un telescopio con obiettivo a specchio diametro 300mm e lunghezza focale 1500mm ha un rapporto focale F di 1500/300 = 5).
Ogni alleggerimento della struttura del dobson finisce quindi per determinare la necessità di dotarlo di maggiori contrappesi.
E questa necessità ci porta ben presto di fronte al “nulla di fatto” dal lato pratico, consistente nell’alleggerire la struttura ….per dover portare comunque con se tanti pesi di bilanciamento quanto è l’alleggerimento operato.
Forse l’unica soluzione tecnica in grado di non cancellare il beneficio dell’alleggerimento, consiste nella trasformazione dei contrappesi (che sono di fatto dei carichi statici), in carichi dinamici forniti dalla trazione di molle, oppure di elastici in gomma (per questi ultimi vedi quì un esempio pratico di bilanciamento di telescopio leggero: https://www.grattavetro.it/ri-bilanciamento-dinamico-con-elastici-di-telescopio-dobson-light/), ed in casi estremi alla installazione sul telescopio di un freno di stazionamento https://www.grattavetro.it/costruzione-dobson-light-300f6-con-freno-a-disco-fase-1-realizzazione/.
E’pur vero che certi contrappesi “estemporanei” si trovano facilmente (Nelle oasi sahariane usavo per questo scopo le mie pedule, che con i loro lacci lunghi permettevano di essere appese alla montatura a pantografo per binocolo su cavalletto). Ma si può fare di molto meglio trasformando i carichi statici in dinamici, per raggiungere ugualmente l’equilibrio di uno strumento da trasportare a mano, o a spalla in uno zainetto.
Molti “addetti ai lavori” d’oltreoceano, per quel motivo, hanno sostituito i pesi allo specchio primario con una coppia di molle di trazione, una per lato del telescopio. Principio meccanico che ho visto applicato anche al Sumerian Alkaid europeo, anche se la trazione adeguata non la fa l’elasticità di una molla, ma quella di un elastico in gomma.
Le due molle di tiro agiscono su ciascuno dei due cuscinetti altitudinali a mezza luna del dobson, in modo che assieme forniscono una forza dinamica equilibratrice, che deve crescere col crescere dell’angolo di inclinazione dello strumento.
COME CONSEGUIRE IN PRATICA L’OBIETTIVO DEL BILANCIAMENTO
Le molle idonee sono quelle del tipo a TRAZIONE (cioè con la spirale chiusa che le rende “pre-caricate” ed estensibili più efficientemente delle molle classiche a compressione con spire distanziate (non idonee per questo utilizzo).
Le molle richiedono una forza direttamente proporzionale al loro allungamento relativo.
Mentre invece per equilibrare un dobson occorre che la forza di bilanciamento della molla sia minima quando lo strumento punta allo zenit, e vada aumentando fino al massimo che si dovrà avere in corrispondenza della posizione orizzontale del telescopio.
E questo andamento crescente rispecchia fedelmente il crescere del coseno dell’angolo di puntamento…In quanto, in parole povere, riconosciamo che il coseno del nostro angolo è rappresentato dalla proiezione sull’Asse orizzontale del suo vettore, che cresce in lunghezza (cioè in forza) man mano che si inclina lo strumento, come mostrato dalla precedente immagine.
Ciascuna molla va collegata con un estremo fisso alla parte bassa del “rocker box”, mentre il capo mobile va collegato ad un cavetto d’acciaio che raggiunge l’estremo della vicina mezza luna/cuscinetto di altitudine attraverso il rinvio di una puleggia di deviazione.
La puleggia interposta, e il suo diametro (che più è piccolo e più aumenta la resistenza utile) ha proprio lo scopo di rinviare il tiro in modo che esso cresca forzatamente col crescere del coseno dell’angolo di inclinazione dello strumento.
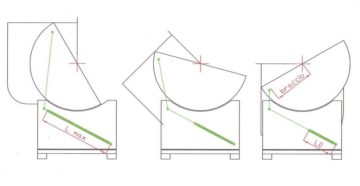
La forza di trazione delle molle sui due lati del telescopio, è zero nella immagine a destra quando il telescopio punta allo zenit, ed aumenta nelle immagini verso sinistra, con l’aumentare della inclinazione, secondo l’aumento del coseno del suo angolo
Ciascuna delle due molle (in verde nella immagine) installate sui due lati del telescopio, si farà carico di metà del peso totale da riequilibrare.
Per maggiore comprensibilità credo sia utile che esponga l’esempio pratico di applicazione su uno dei miei dobson in seguito al cambio di un pesante specchio Hubble, con uno più leggero.
In prima battuta occorre montare lo strumento completo di tutto l’hardware di osservazione che interessa bilanciare. E poi fatto ciò, occorre rilevare in pratica mettendo dei pesi, quanti kg di contrappeso si rende necessario aggiungere dietro la casa del primario per recuperare l’equilibrio generale.
Nella mia verifica trovai che servivano 2,3 kg.
Ciascuna delle mie due molle avrebbe dovuto quindi contrapporre un “tiro” massimo di (2,3/2=) 1,15 kg
Prendendo ora in esame il raggio dei cuscinetti di altitudine, che nel mio caso erano di 260mm, decisi che avrei potuto sfruttare in modo utile 240mm di tale lunghezza per agganciare l’estremo della funicella collegata alla molla di trazione.
(Tuttavia, lungo tutto quel tratto di 240mm avrei avuto la possibilità di spostare a piacere il fissaggio della trazione, potendo con ciò variare la lunghezza del “braccio” di forza, ed assicurarmi il conseguimento a fine lavoro, di una regolazione molto fine della forza di equilibrio desiderata).
Quindi, la forza di 1,15kg divisa per il suo “braccio” di 240mm, mi fornì la rigidezza che la molla adeguata doveva possedere (Il rapporto fra carico e allungamento è infatti chiamato tecnicamente rigidezza della molla) cioè più o meno (1150g/240mm= ) 4,8 grammi per ogni millimetro di allungamento.
Questo voleva dire che la molla idonea, caricata con un peso di 100 grammi, si sarebbe dovuta allungare di circa 20,8mm…o caricata di un chilogrammo si sarebbe allungata di 20.8cm:
Il secondo ed ultimo parametro pratico da rilevare, fu la misura di massima estensione che la molla idonea avrebbe dovuto raggiungere (Lmax), senza deteriorarsi quando lo strumento fosse passato a puntare dallo zenit all’orizzonte.
L’allungamento necessario lo si ottiene misurando l’escursione della distanza fra il centro della puleggia di rinvio, e il terminale di ancoraggio del cavetto al cuscinetto di altitudine, durante la inclinazione dello strumento dallo zenit all’orizzonte.
Questi tre dati sono il minimo indispensabile per eseguire con successo un bilanciamento.
Con gli ultimi due, i costruttori delle molle (oltre che fornirci i terminali di esse fatti ad anello intero, centrati come è conveniente per questo uso), sono in grado di dimensionare esattamente queste ultime.
Infatti: Coll’allungamento desiderato il fornitore è in grado di determinare il diametro ottimale delle spire della molla (il cui diametro più è piccolo e più la molla avrebbe vita breve per la troppo forte torsione) ; e col carico unitario, può determinare il diametro del filo di acciaio che utilizzerà tenendo conto del modulo di elasticità tangenziale G dell’acciaio armonico in uso.
Se le molle non sono fornite da un fabbricante, ma sono ad esempio acquistate in un “fai da te”, le cose sono un po’ più complicate dai compromessi empirici che bisogna trovare strada facendo, mettendone magari in serie (per conseguire allungamenti notevoli) o in parallelo (per aumentarne la forza).
In questi casi, per aggirarsi nell’ambiente occorre farsi “l’occhio”, e per questo serve conoscere le regole costruttive generali che riguardano le molle, che sono le seguenti:
In genere il diametro del filo delle molle che fanno al caso dei bilanciamenti dobsoniani dell’entità di qualche chilo, è fra 1mm e 1,5mm.
Di conseguenza una seconda regola tecnica degli addetti ai lavori stabilisce il diametro della spirale della molla preso a centro filo, pari a dieci volte il diametro del filo.
Ma il costruttore può variare questo diametro della spirale, in funzione dell’allungamento massimo raggiungibile.
Infatti maggiore è il diametro della spirale e minore è la sollecitazione a torsione sul filo della molla, per non andare troppo vicino al limite di elasticità a torsione, che accorcerebbe la vita della molla.
Normalmente una molla di trazione viene progettata per poter essere sollecitata in estensione fino a 2,5 o max a 3 volte la sua lunghezza a riposo.
Nel mio telescopio desideravo delle molle in grado di potersi allungare di 380mm per sfruttare il massimo braccio della mia leva da 240mm (sui 260 di raggio dei cuscinetti altitudinali) e che avessero una rigidezza di 4.8 grammi/millimetro.
Con questi dati di input il fornitore mi calcolò e fornì le molle in filo diametro 1,2mm, ciascuna lunga 150mm e con diametro esterno 12mm.
Tutto il lavoro quindi può essere fatto in modo pratico, senza bisogno di fare calcoli preventivi.
Tuttavia, per chi non volesse privarsi di questo piacere di ricavarsi i dati, le formule della rigidezza e della estensione della molla a spirale sono le seguenti, dove:
G è il modulo di elasticità a torsione (dipende dalla qualità del filo, ma vale in genere circa 8000);
D è il diametro del filo;
r è il raggio della spira a centro filo
Rigidezza = π•G•D filo^4
Estensione = Rigidezza / (32•raggio spira^2 •Lunghezza molla mm)
L’estensione indica i Kg necessari per comprimere o estendere di 1 mm una molla
Chi volesse approfondire può trovare un bell’articolo di Tom Krajci su Sky and telescope Novembre 1999 pagina 130 “A balancing act for dosbsonian telescopes”