I sferometro - The Grattavetro

The spherometer is a measuring instrument used in the machining of an astronomical mirror, to verify the depth of the sagitta, and then the radius of curvature of the surface under examination.
The instrument itself is not complicated, It's consists of a rigid supporting structure on which are placed 3 support feet arranged so as to be located at the vertices of an equilateral triangle, and in the center is positioned a screw device or a dial indicator to measure the depth of the excavation.

Knowing the radial distance from the 'central rod legs and the measured depth, you can, by means of suitable mathematical formulas, back to the curvature of the surface of the radius value.

The mobile measuring rod, If screw type system, is generally fromed by a screw whit lead equal to 1 mm integral with a graduated disc having 100 divisions, which then allows a reading of the extent of the order of hundredths of a millimeter.
The three feet instead, can be formed by sharp rods, or three spheres of known diameter. The substantial difference between the two solutions lies in the different formulas that must be used to calculate the final result.

In particular, the formulas to be used are:

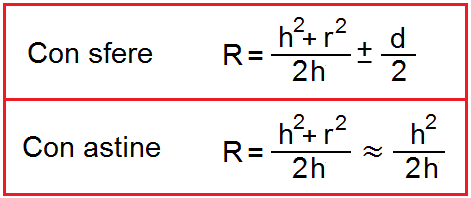
being:
R = Radius of curvature of the surface (2 Sometimes the focal)
h = measured value of the sagitta
r = radial distance from the central srew-legs
O = Diameter of the balls used

The ± present in the formula for calculating the radius of curvature for the spherometer with spheres it must be understood as a sign + if it is analyzing a concave surface, While as a sign – if it is analyzing a convex surface.

Another variant of the instrument is shown below, in which instead of the three bearings is a tubular cylindrical section. In this variant, if you analyze a concave surface to rest on it will be the outer circular ring, while if one analyzes a convex surface to rest on it will be the inner ring. It will be important, therefore, to use the correct radius value (r) in the formula, depending on the case.

HOW TO USE IT

The first operation to perform is to verify the zeroing of the instrument going to making a measurement on a flat surface.

Proceed with the measurement of the surface to be analyzed.
If you have a spherometer dial indicator measurement will take place immediately and and without fatigue, while if you have one of srew spherometer, you should turn the screw to get it down until its tip comes in contact with the surface.
The techniques to figure out when the contact occurred primarily 2:
In the first, Once you get in contact and you continue to turn the screw, the entire spherometer will tend to rotate on itself, then return back slightly until it reaches the ideal position (sensibility 3-5 cents mm); in the second, if also just slightly exceeds,, the value of the sagitta, one of the legs will detach from the surface of the glass. If pressure is applied alternately above the supporting feet you should feel a ticking (as a wobbly table), then go back up to the disappearance of the effect (sensibility 1-2 cents mm).

At this point read the measurement and using the correct formula to calculate the radius of curvature of the surface (or focal dividend 2 the result).
Nell 'example given the value of the arrow is just over 0.81 mm (being the concave surface of the dipstick is decreased with respect to the zero position, then the pointer is moved in a counterclockwise direction).
Applying the above formula, the result of the radius of curvature (R) totaled 920.6 mm (having the spherometer under examination r = 39mm and d = 7.95mm).

EXAMPLE OF ONE SPHEROMETER autocostruito:

For the construction of this spherometer I used as a base of support in a fairly sturdy plastic gear and of appropriate diameter recovered from an old copier..

I have used this support because as you can see from the image below has a circular area on the outside of delimited by two edges that allow me to position accurately (at least to the radial level) the three spheres of steel support. Is 12 radial ribs that allow me to easily place the beads at 120 ° to each other.

To lock in position the comparator instead, it's drill a hole of adequate size to allow passage of the outer Rod cursor that has been clamped into place by a transversal screw.

And this is the spherometer competo positioned on a flat surface for zeroing:

Giulio TiberinI

13 February 2017

Comments (2)

deabu

27 March 2016
Log in to Reply

In the first phase of lavodazione of a parabolic mirror, When you are working with a large grain to dig the mirror and reach the desired arrow, the ball is far from perfect. At this stage, I believe it is appropriate to use one spherometer that it rests on the edge of the mirror or as close as possible to it, so as to eliminate any measurement errors due to a still imperfect sphere. Obviously, this problem does not exist or is minimal in the subsequent processing stages, When, that is, We are working with fine grains, and the ball is now formed.
On the other hand it is also true that one spherometer with three support points (or support disk) with small diameter, or at least a smaller diameter than that of the mirror, It allows us to make a first verification of the regularity of the ball: It will be sufficient to carry out several measurements in different points of the mirror and verify that the measurement returned by the instrument is constant. Contrary, the ball will be still inaccurate.
I conclude by saying that, having the ability to build itself one spherometer, It would be interesting to produce at least two, one with sufficiently broad support to be positioned on the edge of the mirror and one with more supports “close”: in this way I will have two instruments useful in two different stages of processing, that will also allow us to compare, and then to verify the measurements in the advanced stages of processing.
Giulio TiberinI

13 February 2017
Log in to Reply

It should however keep in mind that the spherometer is useful only when it has some assurance that the curved surface to be measured and objectively at least one uniform spheroid, otherwise there is no guarantee that the measured one is really a spherical surface.

In fact, the detection of the radius of curvature belonging to the sphere incognita which connects the central point of measurement of the spherometer, to the diameter of the plane identified by its three peripheral feets, It is correct only if the surface between the measuring points is spherical.

From the perspective of "do it yourself" the amateur astronomer who creates his own mirror, spherometer is not necessary, because the only guarantee that the curve produced by manual labor is a good spheroid, It is given by the disappearance of the persistent air bubble after the roughing because trapped between the mirror and the tool.
In fact, until the air bubble is present, is a sign that the two mirror surfaces and tool do not have the same radius of curvature.

According to the same Foucault tips (who was the advocate of the feasibility by hand of glass mirrors , in an era in which only metal seemed possible to achieve them), to get surely to a good sphere, must be put into practice only 5 following rules:
– Use a tool full diameter;
– Having the foresight to apply the amplitude strokes in the forward-backward direction 1/3 Diameter, "center over center" (therefore ooze forward-backward 1/6 the mirror diameter);
– Minding the same time to remain centered with those races in the left-right direction, ie without laterally overflowing (Because the lateral overflow would lead to flare too early the sphere toward the parable, even when it is not perfectly polished; Or to produce a surface flared much over the parable).
– Finally we need to work by turning in small steps around the table,
– rotating well as a little at a time in the opposite direction, the glass that you have in hand.
And it's all.

Given the large amount of strokes that unitaryly remove very little glass, is the statistical analysis of large numbers that applying a similar behavior, It produces good spherical surfaces reaching very high precision machining also freehand, as the small opposing errors cancel each other out.