mi’ útil en este punto, un retiro en las técnicas de procesamiento con las herramientas en el sub-diámetro, en particular, sobre cómo es posible aumentar la curvatura de una o más zonas.
entonces Recordemos el concepto según el cual durante el pasado con el sub-diámetro, áreas externas aumentan su curvatura mientras que el interior de la disminución, lo que quiere decir que durante el pasado generar una “surco” en la superficie, No en el sector central de la zona de mecanizado es más profundo que el resto de la superficie mecanizada.
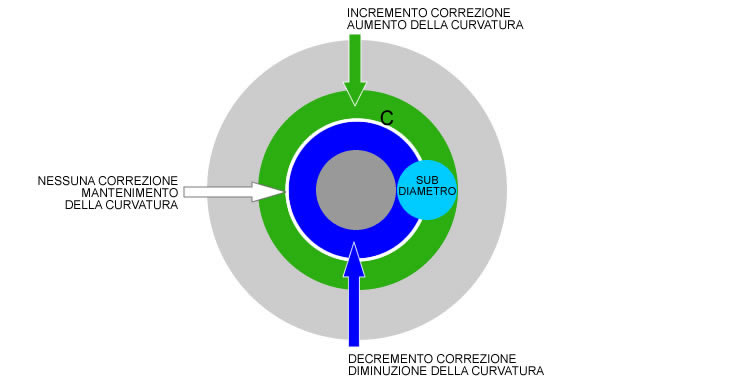
Higo. 1 – Acción sobre el diámetro de la curvatura sub-superficie
teóricamente ( pero no en la práctica ) la única aplicación de esta técnica es suficiente para lograr el resultado deseado. vemos cómo:
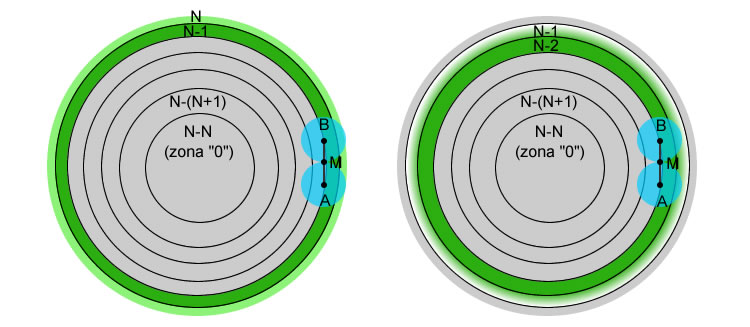
Higo. 2 – Secuencia de los curvatura aumenta en las zonas adyacentes.
asumir norte como el número total de áreas en las que prácticamente dividir nuestro espejo . Así que vamos a tener nuestra sucesión de zonas ( sectores circulares de ancho predeterminado ) a partir del borde hacia el espejo centro: norte, N-1, N-2, ….. , N-N.
Nuestra hipótesis de partida nos dice que la esfera y parábola son coincidentes en el borde, pero teniendo en cuenta que en las pruebas que nunca tendremos una forma de medir la curvatura en el borde, nada nos impide “movimiento” Este punto de tangencia ( Recuerde que puede ser elegido de manera arbitraria en cualquier punto de la sección de partida esférica ) en el centro de la zona más periférica ( norte ) , justo en el punto donde la medida se lleva a cabo.
Tendremos por lo que el centro de la última zona es, por definición, “correcto”, siendo tangente tanto la pelota al perfil parabólico del proyecto y por lo tanto no debe ser trabajado, entonces empezamos a excavar el centro de la zona próxima N-1 hasta que tampoco será tangente al perfil parabólico quería.
Para ello debemos hacer que el área N-1 y su centro más profundo de una de las zonas norte en comparación con la esfera de partida, en otras palabras, necesitamos aumentar la curvatura de la bola inicial pasando de N-1 una norte.
a continuación, aplicar el diámetro antes mencionado de la sub-técnica, Preparamos una herramienta cuyo radio es ligeramente mayor que la distancia entre los centros de dos zonas sucesivas , Vamos a colocar el centro de la herramienta en el borde interior de la zona N-1 y llevará a cabo pequeños paseos de aquí para allá con el patrón circular alrededor de la zona. El resultado será que habremos aumentado la curvatura exactamente entre la zona N-1 ed norte. Haremos la medida de este incremento con un ensayo adecuado, limitándonos sólo para medir la “borrador” de estas dos zonas, y repetimos sesiones con el sub-diámetro hasta que el proyecto de medición no será coincidente con la de la simulación ( calculada matemáticamente o por medio de software ) de nuestra última parábola .
En este punto tenemos dos áreas correctas que la parábola final. a continuación, vamos a pasar a la siguiente zona N-2 y repetir el mismo procedimiento “excavación” y la conexión entre el N-1 y N-2 hasta llevar este también dibujar en el valor correcto.
Vamos a aplicar el procedimiento de forma sucesiva hasta que la última área N-N ( el centro del espejo o “zona 0” ) para asegurar que la última zona “útil” , la NORTE-(N + 1) , que es la primera área central , y las conexiones para la parábola completa.
DENTRO LA “Trompeta del TOLERANCIA”
la generación de la parábola como el aumento de profundización de zonas consecutivas, También puede verse como una sucesión de áreas de flujo “tolerancia” en el gráfico Millies-Lacroix. Para ello hay que recurrir a una pequeña “maquillaje” que nos ayudará en la vista inmediata de lo que vas a hacer.
Nuestra esfera de partida con radios idénticos de curvatura de las zonas ( dibujar = 0 ) insertado en el gráfico ML de un espejo hipotético 300 parabólico mm F4, Tendría una representación similar a este:
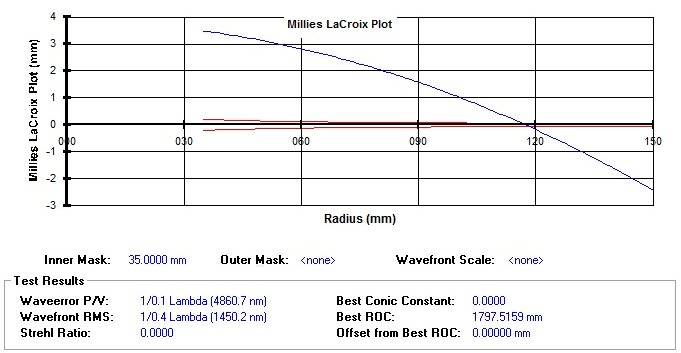
Higo. 3 – Gráfico Millies-Lacroix para una superficie esférica ( la escala se altera para una mejor visualización )
Apliquemos ahora nuestra primera hipótesis, a saber, la de tangencia entre el borde de la esfera y parábola,( en lugar del radio 115 mm como se muestra en la figura) , que es equivalente a traducir la curva ascendente hasta la caída de la centro de radio de curvatura 150 mm en el centro de la trompeta tolerancia:
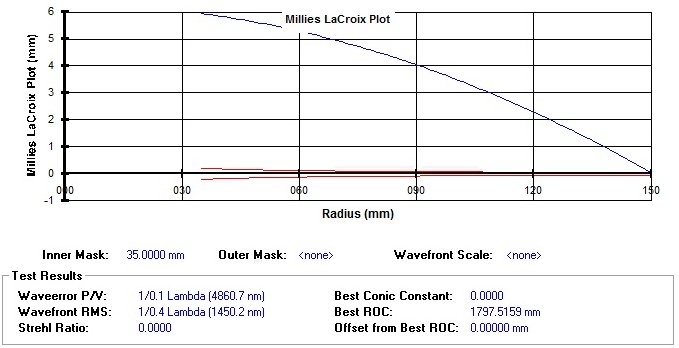
Higo. 4 – Gráfico Millies-Lacroix para una superficie tangente esférica hasta el borde con el paraboloide ideales ( la escala se altera para una mejor visualización )
la traducción ( la “maquillaje” ) que acabamos de hacer en Ml partido Tabla de lo que elegimos hacer en la sección B primera parte de:
B - "Nos acortar" las reflexiones centrales: Es equivalente a decir que, a partir del borde y nos movemos gradualmente hacia el centro aumentará la curvatura del espejo de tal manera que las reflexiones de las zonas centrales convergen más cerca, sólo lo suficiente para hacerlas coincidir con esos dispositivos.
Observando el gráfico configurado de este modo, es bastante intuitiva que, llevar la bola a la parábola, toda la curva entrará en la tolerancia, Por tanto, debemos profundizar en la superficie (“echar abajo” la curva ) comenzando cada vez más desde el borde hacia el centro
Supongamos que hemos calculado los valores exactos de los centros de curvatura de nuestra parábola ideal y trabajamos el espejo de acuerdo con el procedimiento, con lo que primero el radio exacto de curvatura de la zona de N-1 ( en este ejemplo N = 5 ) y luego todos los demás. Esto es lo que debemos esperar en el gráfico ML calculado mediante la prueba de Foucault, es decir, la secuencia de la zona correcciones después de área :
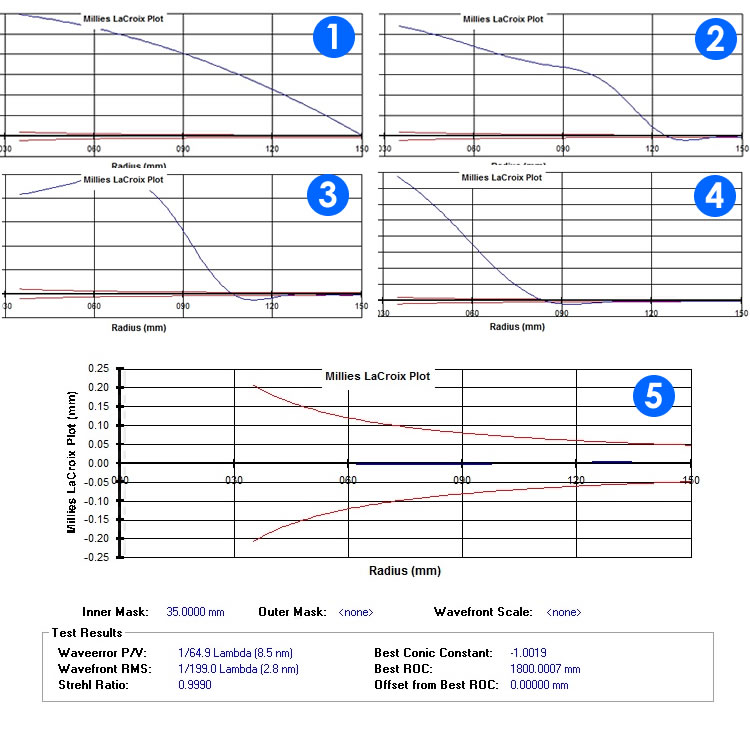
Higo. 5 – Sucesión de puntos de vista zonal.
Teoría a la práctica
Como se ha mencionado, en la realización práctica las cosas no son inmediatos, Intervienen en diferentes elementos de hecho que aconsejan en contra de un enfoque directo, que se encuentran en avance de las soluciones a estos problemas:
- para longitudes focales cortas, el número de áreas a examinar tiene que estar razonablemente alto, cuanto mayor es el número de zonas es menor que la extensión de la herramienta que permite trabajar sólo dos zonas adyacentes sin interferir con el otro, deducible con incrementos de los tiempos de procesamiento.
- El aumento de la curvatura de la zona exterior disminuye en consecuencia la de la zona interior que posteriormente será minuciosa tanto en valor con respecto a la esfera del valor adicional de disminución de la curvatura recién generado.
- cuanto menor es la extensión herramienta, mayor será la probabilidad de generar errores en la superficie locales de corrección difícil, yo “pequeño” sub-diámetro debe utilizarse con moderación , para hacer pequeñas correcciones y una buena experiencia para usar en menos configuraciones “extremo”.
- Es difícil llegar a la medida exacta del sorteo de dos zonas que actúa en una dirección solamente, a saber, solamente el aumento de la curvatura. mi’ probablemente más cercano a la figura ideal excederá ( aunque muy poco ) en el procesamiento y es necesario “volver” es decir, actuando en la dirección opuesta para disminuir la curvatura, con consecuencia directa e inevitable de modificación de la forma también en las zonas adyacentes.
- Este procedimiento no permite una inspección completa de la superficie durante la construcción de la figura, especialmente con las pruebas complementarias como la Ronchi, Se basa en “confianza” que estamos trabajando bien, pero la confirmación vendrá sólo después de completar toda la parábola.
Este último punto puede ser mejor resaltado si simulamos la gráfica de Ronchi prueba correspondiente al área de procesamiento después de fases de área:

Higo. 6 – Simulación de la Prueba de Ronchi para la profundización de la sucesión zonal.
Como se puede ver en la figura 6 , esta metodología, manteniendo buenas premisas iniciales, Que no permite evaluar inmediatamente hasta qué punto el mecanizado en tanto “Stada derecha”, Sólo después de haber llevado todas las zonas personalizadas, vamos a evaluar la corrección de la superficie en su totalidad.
Por tanto, es necesario optimizar esta estrategia a lo largo de los trabajos de construcción de la figura, para hacer posible el control de la calidad de mecanizado durante cada fase, eliminar o al menos reducir al mínimo la posibilidad de errores locales o generales y que todavía permite identificarlos con certeza y de intervenir “sin peligro” si presentassero.
mi’ lo que vamos a encontrar en la tercera parte.