La documentación sobre estas pruebas ópticas interesantes recientes apareció en Internet en los diferentes idiomas de los países donde está más extendido construcción óptica auto-aficionado. Por lo que un texto en italiano, actualmente no existe. por lo tanto, de curiosos y “persona enterada” Pensé que traducir al italiano, Yo uso y la gente como yo, que puedan beneficiarse de ellas, En el siguiente artículo, El original de la que se encuentra en la dirección siguiente: http://www.astrosurf.com/tests/roddier/roddier.htm
La ventaja de esta prueba es que es de tipo fotométrico, y luego se proporciona información sobre el estado del espejo toda la superficie óptica. Pero esta información no es el resultado de las evaluaciones subjetivas mediante la ejecución de la prueba, Al igual que con las pruebas de casi todos ópticas aficionados aplicable, sino que son el resultado de una evaluación objetiva realizada por el equipo sobre la base de dos sesiones de fotos realizada en la imagen de una estrella fugaz en el centro de coordinación intra y extra por el instrumento.
El mismo hecho, sin embargo, que esta interesante prueba se basa en dos tomas de cámara dentro y fuera de un foco del telescopio, Se supone que el telescopio es una herramienta ya construido y operativo.
Que relega el uso de la prueba de interés en una mera evaluación cualitativa de una óptica existente, lo que hace inútil al fabricante “grattavetro” que siempre anhela encontrar una alternativa a la subjetividad inherente evaluación objetiva más o menos en todas las pruebas utilizadas en el parabolizzazione perspectiva, destinado a proporcionar una guía cuantitativa para las correcciones a realizar en diversos ajustes que se suceden en el camino de la fabricación “mejor espejo”, no es “perfecto”.
Esta es una prueba “subproducto” de la tecnología”óptica adaptativa”, desarrollado, (y desde hace bastante tiempo “clasificado” con interés militar) para local y temporalmente deformar las propiedades ópticas de telescopios muy grandes con el fin de compensar instantáneamente por los daños causados por la turbulencia atmosférica, eliminando prácticamente la última en tiempo real, ya que se produce en el curso de la observación.
Tal óptica adaptativa proporciona para la transformación de la imagen capturada desde el telescopio en un algoritmo matemático que identifica la presencia de una cierta aberración óptica local de, y se corrige con actuadores mecánicos que generan un signo opuesto.
El estudio de las aberraciones ópticas, y su descripción en términos matemáticos enormemente facilitada por la informática, Esto significa que el mismo principio se puede aplicar en esta prueba Roddier para la evaluación de la óptica también a nivel amateur, con una precisión e integridad interesante.
Aquí está el artículo:
(Claude y su esposo François Roddier trabajaron en el observatorio en Hawai, específicamente en la alta resolución angular. Ahora se retiraron. Sus trabajos sobre óptica adaptativa y activos fueron una contribución a la mejora del rendimiento de los telescopios muy grandes. )
1. Principio teórico
2. Un ejemplo para comprender mejor
3. Un ejemplo práctico
Como se sabe, con la prueba visual escribir la prueba estrella, se puede obtener información sobre los defectos ópticos de un instrumento, observando las dos imágenes borrosas de una estrella. La prueba Roddier generaliza este concepto con un programa de ordenador realizando un análisis fotométricos y geométricos automáticas dos fotografías realizadas en el comercio intra y extrafocal, obtenida con una cámara CCD.
• El programa de ordenador está disponible gratuitamente en la Web
• Ver el progreso del proyecto para unir el artículo original se informó anteriormente, y descargar el programa de WinRoddier.
1. Principio teórico
En primer lugar consideramos una herramienta perfecta, que proporciona a su enfoque de la imagen de una estrella. Entonces registraron dos imágenes defocalizzate; una a la distancia "l" hacia adelante , sobre el fuego (hacia el interior del instrumento); y una vez en el mismo "l" pero la distancia de vuelta ante el fuego (hacia el exterior del instrumento)
La pupila de entrada es iluminada de manera uniforme (intensidad I0 ), y sólo una pequeña porción de esta pupila (Figura 1): El flujo luminoso que pasa a través de esta porción pequeña intrafocale ilumina la imagen sobre una superficie más pequeña, con una intensidad I1, y la imagen extrafocal en un I2 superficie igual a la de la imagen intrafocale, ya que las dos imágenes son tomadas a la misma distancia del fuego. El I0 inicial intensidad se por lo tanto "concentrada" de la misma forma en las dos imágenes, y que tiene:
I1 = I2
Supongamos ahora que el frente de la onda de salida de la pupila de entrada tiene un defecto: En la superficie de la pupila pequeña considerado previamente, aparece curvada (Figura 2) .El fuego real es, para esta parte de la pupila, situada en frente del fuego del instrumento. En la imagen así intrafocale, la luz es más concentrada que en la extrafocal.
I1 > I2
prueba de col di Roddier se compara ahora I1 a I2 gracias al cálculo de la cantidad I2 - I1, con el fin de volver a los defectos en el frente de onda.

Higo. 2 : Prueba Roddier de producto defectuoso: El I2 intensidad I1et son diferentes. Esta diferencia de intensidad está relacionada con la curvatura del frente de onda.
La teoría muestra que si se tiene en cuenta la imagen en su conjunto (y no pequeñas porciones como anteriormente), la señal calculada mediante la realización de la resta de las dos imágenes intra y extra, Es proporcional a la laplaciana del frente de onda.
• El frente de onda Laplaciano (el cálculo de lo que implica la segunda derivada), Está relacionado con la curvatura del frente de onda (véase la Figura 2)
NOTA: (el operador de Laplace matemática o laplaciano, cuyo nombre se debe a Pierre Simon Laplace, está un segundo operador diferencial orden define como la divergencia del gradiente de una función en un espacio euclidiano).
El problema en nuestro caso es diferente: Tenemos que reconstruir el frente de onda de su laplaciano. Esto se realiza con la ayuda de un programa informático especializado que, marcas, además del cálculo de la Laplaciano, numerosas correcciones geométricas y fotométricas destinados a determinar las aberraciones de frente de onda.
Estos cálculos se realizan a menudo en tiempo real para los profesionales (Activo en sistemas ópticos modernos, o adaptativo) ejecutar el Roddier prueba para deformar la superficie óptica de los espejos grandes con el fin de corregir las aberraciones del frente de onda.
2. Un ejemplo para comprender mejor
La figura 3 Se representa la región de fuego de una herramienta abollado de aberración esférica (en sobrecorrección) : Los rayos centrales convergen con una longitud focal más corta que la de los rayos marginales. La aberración de frente de onda correspondiente a esto se traduce en niveles de gris (higo. 4UNA): El frente de onda es cóncava en el centro, y replicó en el borde. La imagen de la Figura 4B representa el laplaciano de este frente de onda.

Higo. 3 : región de fuego de una herramienta que presenta una aberración esférica (sobrecorrección). La placa de destino tiene una longitud focal más larga que la de su centro. palabras clave + y – referirse a las diferencias de intensidad luminosa en las imágenes intra y extra, en relación con una intensidad distribuida de manera uniforme en ausencia de aberración (el caso de la figura 1).

La figura 4A: frente de onda – Figura 4B: frente de onda Laplaciano – Un fig.5. intrafocale foto – Fig 5B. extrafocal foto
Consideremos ahora las imágenes intra y extra de la figura 5
• Ubicación central de las imágenes : En intra hay un exceso de intensidad (conocido +) y extras hay un defecto (conocido -) porque los rayos centrales convergen más cerca de la imagen intra (ver figura 3).
• Imagen de Zona Marginal : En intra hay una intensidad defecto (notado el signo -) mientras que en adicional hay un exceso de (notado el signo +) debido a que los rayos marginales convergen cerca de la Imagen Extra (ver figura 3).
Cuando se lleva a cabo la sustracción de las dos imágenes S, se obtienen los siguientes resultados:
• Zona Central : Un exceso de intensidad como (+) – (-) = (+)
• zona marginal : Un defecto en intensidad como (-) – (+) = (-)
De hecho, esto es lo que observamos en el frente de onda imagen Laplaciano (Figura 4B).
El frente de onda está relacionada operador laplaciano, S a la señal obtenida al restar las dos imágenes intra y extra .
(Lo que hemos visto hasta ahora aquí es un ejemplo sencillo de fijar las ideas, es decir, que no están bajo ninguna circunstancia una demostración !)
3. Un ejemplo práctico
Una vez que hemos tomado medidas para reconstruir el frente de onda, se remonta a los valores de los principales aberraciones de descomposición de la misma frente de onda Zernike polinomios.
Estos polinomios se definen funciones matemáticas en un disco, que puede ser ligado a las principales aberraciones.
Por ejemplo,, la imagen de la figura 4 es la representación del polinomio de Zernike se vincula a la aberración esférica (leer más detalles sobre Zernike polinomios). La adición de más polinomios, se puede reconstruir una aberración de frente de onda tanto afectada por. Inversamente, un frente de onda medido se puede ajustar a diferentes polinomios, con el fin de rastrear las aberraciones.
A modo de ejemplo, reproducimos aquí un extracto del análisis de un comercio Schmidt-Cassegrain (buena calidad). 5A es la imagen del frente de onda reconstruido a partir de programa informático EF a partir de dos imágenes intra y extra de focales.
la siguiente mesa 1 Muestra los valores RMS de una aberración, y la Figura 5B es la imagen del frente de onda reconstruido utilizando los valores de las aberraciones y la 22 primeros polinomios de Zernike. La utilización de estos 22 polinomios permite encontrar los principales aberraciones y reconstruir la forma general del frente de onda.
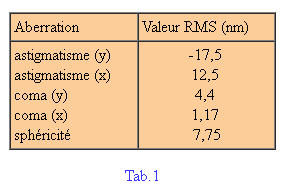
Fig.5A: Wavefront calculado con el Programa EF a partir de una imagen intrafocal y una
extrafocale.
Fig.5B: Frente de onda reconstruido desde 22 los polinomios son Zernike, utilizando valores rms
aberraciones proporcionadas por el programa EF.
El gráfico 1 es un extracto de estos 22 valores. (La unidad de medida es el nanómetro.).
(NOTA: Más explicaciones interesantes y encontrar software actualizado en la web mediante la búsqueda: “Proyecto WinRoddier” su Astrosurf – y discusión “Prueba óptica (Roddier)” sul forum Noche nublada).

