La documentazione su questo recente ed interessante test ottico è apparsa in internet nelle diverse lingue dei paesi ove è più diffusa l’auto-costruzione ottica amatoriale. Quindi un testo in italiano, al momento non esiste. Perciò, da curioso e “addetto ai lavori” ho pensato di tradurre in italiano, a mio uso e di chi come me può trarne vantaggio, il seguente articolo, il cui originale si trova al seguente indirizzo: http://www.astrosurf.com/tests/roddier/roddier.htm
Il vantaggio di tale test è che esso è di tipo fotometrico, e quindi fornisce informazioni sullo stato della INTERA superficie ottica dello specchio. MA tali informazioni non sono il frutto di valutazioni soggettive da parte dell’esecutore del test, come avviene per quasi tutti i test ottici applicabili amatorialmente, ma sono frutto di una valutazione oggettiva eseguita dal computer sulla base dell’analisi di due riprese fotografiche eseguite sulla immagine di una stella ripresa in intra ed extra focale dallo strumento.
Il fatto stesso però che questo interessante test sia basato su due riprese fotografiche in intra ed extra focale di un telescopio, presuppone che quel telescopio sia uno strumento già costruito ed operativo.
Il che relega l’interesse all’uso del test ad una mera valutazione qualitativa di un ottica esistente, rendendolo inutilizzabile al costruttore “grattavetro” che da sempre anela trovare una alternativa oggettiva alla soggettività di valutazione insita più o meno in tutti i test utilizzabili nel corso della parabolizzazione di un’ottica, finalizzati a fornire una guida quantitativa alle correzioni da apportare nei vari ritocchi che si susseguono sulla via della fabbricazione dello “specchio migliore”, se non “perfetto”.
Questo test è un “sottoprodotto” della tecnologia dell”ottica adattativa”, sviluppata, (e per parecchio tempo “classificata” con interesse militare) per deformare localmente e temporaneamente le ottiche dei grandissimi telescopi al fine di compensare istantaneamente il danno causato dalla turbolenza atmosferica, eliminando di fatto quest’ultima in tempo reale, man mano che si presenta nel corso della osservazione.
Tale ottica adattativa prevede la trasformazione della immagine captata dal telescopio in un algoritmo matematico che individua la presenza di una certa aberrazione ottica locale, e la corregge con attuatori meccanici che ne generano una di segno opposto.
Lo studio delle aberrazioni ottiche, e la loro descrizione in termini matematici enormemente facilitata dagli elaboratori elettronici, fa si che lo stesso principio possa essere applicato in questo test di RODDIER per la valutazione delle ottiche anche a livello amatoriale, con una precisione e completezza interessanti.
Ecco l’articolo:
(Claude e suo marito François Roddier hanno lavorato presso l’osservatorio delle Hawaii, specificamente sulla alta risoluzione angolare. Essi sono attualmente in pensione. I loro lavori sull’ottica adattativa e attiva sono stati un contributo al miglioramento delle prestazioni dei grandissimi telescopi. )
1. Principio teorico
2. Un esempio per capire meglio
3. Un esempio pratico
Come è noto, con test visuali tipo lo star test, si possono ottenere informazioni sui difetti ottici di uno strumento, osservando le due immagini sfocate di una stella. Il test di Roddier generalizza questo concetto realizzando con un programma informatico una analisi fotometrica e geometrica automatica di due fotografie eseguite in intra ed extrafocale, ottenute con una camera CCD.
• Il programma informatico è disponibile gratuitamente sul Web
• Vedere l’avanzamento del progetto al link dell’articolo originale riportato più sopra, e scaricare il programma WinRoddier.
1. Principio teorico
Per cominciare consideriamo uno strumento perfetto, che fornisce al suo fuoco l’immagine di una stella. Si registrano quindi due immagini defocalizzate; l’una alla distanza “l” in avanti , oltre il fuoco (verso l’interno dello strumento); ed una alla stessa distanza “l” ma indietro prima del fuoco (verso l’esterno dello strumento)
La pupilla di entrata è illuminata in maniera uniforme (Intensità I0 ), e altrettanto una piccola porzione di questa pupilla (fig.1): Il flusso luminoso che passa per questa piccola porzione illumina l’immagine intrafocale su una superficie più piccola, con una intensità I1, e l’immagine extrafocale su una superficie I2 uguale a quella della immagine intrafocale, poiché le due immagini sono prese alla medesima distanza dal fuoco. L’intensità iniziale I0 si trova dunque “concentrata” allo stesso modo sulle due immagini, e si ha:
I1 = I2
Supponiamo ora che il fronte d’onda uscente dalla pupilla di entrata abbia un difetto: Sulla superficie della piccola pupilla considerata precedentemente, esso appare incurvato (fig.2) .Il fuoco reale è, per questa porzione di pupilla, situato davanti al fuoco dello strumento. Sulla immagine intrafocale quindi, la luce è più concentrata che su quella extrafocale.
I1 > I2
Col test di Roddier si compara ora I1 a I2 grazie al calcolo della quantità I2 – I1, in modo da risalire ai difetti del fronte d’onda.

Fig. 2 : Test di Roddier di uno strumento difettoso: Le intensità I1et I2 sono differenti. Questa differenza d’intensità è legata alla curvatura del fronte d’onda.
La teoria mostra che se si considera l’immagine nel suo insieme (e non delle piccole porzioni come qui sopra), il segnale calcolato effettuando la sottrazione delle due immagini intra ed extra, è proporzionale al Laplaciano del fronte d’onda.
• Il Laplaciano del fronte d’onda (il cui calcolo implica le derivate seconde), è legato alla curvatura di questo fronte d’onda (vedi fig.2)
NOTA: (l’operatore matematico di Laplace o Laplaciano, il cui nome è dovuto a Pierre Simon Laplace, è un operatore differenziale del secondo ordine definito come la divergenza del gradiente di una funzione in uno spazio euclideo).
Il problema in questo nostro caso è diverso: Bisogna ricostruire il fronte d’onda a partire dal suo Laplaciano. Questo si esegue con l’aiuto di un programma informatico specializzato che, effettua, oltre al calcolo del Laplaciano, numerose correzioni geometriche e fotometriche tese a determinare il fronte d’onda e le sue aberrazioni.
Tali calcoli sono spesso eseguiti in tempo reale da professionisti (nei moderni sistemi di ottiche attive, oppure adattative) che eseguono il test di Roddier per deformare la superficie ottica dei grandissimi specchi al fine di correggere le aberrazioni del fronte d’onda.
2. Un esempio per comprendere meglio
La figura 3 rappresenta la regione del fuoco di uno strumento intaccato dalla aberrazione sferica (in sovracorrezione) : I raggi centrali convergono con una distanza focale più corta di quella dei raggi marginali. Il fronte d’onda corrispondente a questa aberrazione è tradotto in livelli di grigio (fig. 4A): Il fronte d’onda è concavo al centro, e ribattuto al bordo. L’immagine della figura 4B rappresenta il Laplaciano di questo fronte d’onda.

Fig. 3 : Regione di fuoco di uno strumento presentante una aberrazione di sfericità (sovra-correzione). Il bordo dell’obiettivo ha una distanza focale più lunga di quella del suo centro. I segni + e – si riferiscono alle differenze d’intensità luminosa sulle immagini intra ed extra, in rapporto a una intensità uniformemente ripartita in assenza d’aberrazione (caso di figura 1).

Fig.4A: Fronte d’onda – Figura 4B: Laplaciano del fronte d’onda – Fig.5 A. Immagine intrafocale – Fig 5B. Immagine extrafocale
Consideriamo ora le immagini intra ed extra di figura 5
• Zona centrale delle immagini : In intra c’è un eccesso di intensità (notata +) e in extra vi è un difetto (notato -) perchè i raggi centrali convergono più vicino alla immagine intra (vedi figura 3).
• Zona marginale delle immagini : In intra vi è un difetto di intensità (notato col segno -) mentre in extra ve ne è in eccesso (notato col segno +) poiché i raggi marginali convergono più vicino alla immagine extra (vedi figura 3).
Allorché si effettua la sottrazione S delle due immagini, si ottengono i seguenti risultati:
• Zona centrale : Un eccesso d’intensità poichè (+) – (-) = (+)
• Zona marginale : Un difetto d’intensità poichè (-) – (+) = (-)
Ciò in effetti è quello che osserviamo sulla immagine del Laplaciano del fronte d’onda (figura 4B).
Il fronte d’onda è legato dall’operatore Laplaciano, al segnale S ottenuto sottraendo le due immagini intra ed extra .
(Ciò che abbiamo visto fin quì è una semplice illustrazione per fissare le idee, non è cioè in nessun caso una dimostrazione !)
3. Un esempio pratico
Una volta che si abbia provveduto a ricostruire il fronte d’onda, si può risalire ai valori delle principali aberrazioni scomponendo quello stesso fronte d’onda in polinomi di Zernike.
Questi polinomi sono funzioni matematiche definite su un disco, le quali possono essere legate alle principali aberrazioni.
Per esempio, l’immagine di figura 4 è la rappresentazione del polinomio si Zernike legato alla aberrazione di sfericità (leggere più dettagli sui polinomi di Zernike). Sommando più polinomi, si può ricostruire un fronte d’onda affetto da altrettanta aberrazione. Inversamente, un fronte d’onda misurato può essere regolato a diversi polinomi, in modo da risalire alle aberrazioni.
Come esempio riproduciamo qui un estratto della analisi d’uno Schmidt-Cassegrain del commercio (di buona qualità). La figura 5A è l’immagine del fronte d’onda ricostruito dal programma informatico EF a partire da due immagini intra et extra focali.
La seguente tabella 1 riporta i valori RMS di qualche aberrazione, e la figura 5B è l’immagine del fronte d’onda ricostruito utilizzando i valori delle aberrazioni e i 22 primi polinomi di Zernike. L’utilizzazione di questi 22 polinomi permette di ritrovare le principali aberrazioni e di ricostruire la forma generale del fronte d’onda.
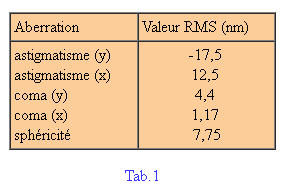
Fig.5A: Fronte d’onda calcolato col Programma EF a partire da una immagine intrafocale ed una
extrafocale.
Fig.5B: Fronte d’onda ricostruito a partire da 22 polinomi si Zernike, utilizzando i valori rms
delle aberrazioni fornite dal programma EF.
La tabella 1 è un estratto di questi 22 valori. (L’unità di misura è il nanometro).
(NOTA: Interessanti ulteriori spiegazioni e reperimento software aggiornato sul web ricercando: “Project WinRoddier” su Astrosurf – e discussione “Optic testing (Roddier)” sul forum Cloudy night).

