Come descritto nel precedente articolo dal titolo “Fase preparatoria al test di Foucault”, Abbiamo preparato il locale, allineato specchio e tester sui loro tavoli e supporti, lasciato acclimatare lo specchio per raggiungere il sicuro equilibrio termico con la temperatura ambiente del locale, ed ora siamo pronti a cominciare la prima sessione del test.
Prendiamo il taccuino in cui avevamo registrato la tabellina di 4 righe e 5 colonne copiata dalla maschera di Couder
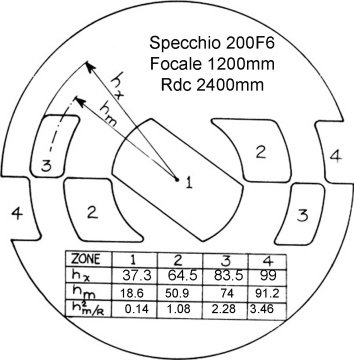
Dove i valori di hx e di hm di ogni zona (vedi di quali raggi si tratta nella immagine della maschera quì sopra) erano dati di costruzione della maschera stessa, mentre nel calcolo di hm 2 /R compare R, che è il raggio di curvatura di 2400 mm, corrispondente alla focale stimata di 1200 mm del nostro specchio, che eventualmente correggeremo quando la misureremo in modo esatto al millimetro.
Contrassegniamo la pagina del taccuino che riguarda il test n°1, come pagina n° 1, e continuiamo le fincature verticali delle colonne della tabellina proseguendo le loro linee fino a fondo pagina, come nella immagine seguente. (Ma, come vedremo, per agevolare il disegno del grafico finale, è meglio se le 4 colonne che riguardano le 4 zone, vengono fin da subito impostate con larghezza eguale di 10 quadretti).

Accendiamo la sorgente e ALLINEIAMO LAMA E FENDITURA
Attenzione che da questo momento in poi è importante vigilare che la posizione del tester rispetto allo specchio in esame, conservi sempre il suo allineamento, man mano che esso viene perfezionato portando la lama del coltello a “tagliare” i raggi luminoso provenienti dal centro del raggio di curvatura della zona centrale dello specchio, che è il punto di partenza del test di Foucault.
Ci mettiamo quindi in posizione di osservazione dietro il tester.
Siccome noi avevamo posizionato il tester allineato allo specchio e già assai “vicino” al raggio di curvatura 2400 mm appartenente alla sua lunghezza focale, guardando lo specchio da dietro la lama del tester, lo vediamo completamente illuminato; cioè vedremo che la luce della fenditura, posta a quella distanza “vicina” al raggio di curvatura, viene diffusa su tutta la superficie (cosa che diversamente non avviene).
NOTA: Per vedere come si esegue in pratica l’allineamento fra specchio e tester, si consiglia la visione di 4 minuti (impostandolo manualmente dal punto “1 ora 04 minuti”, al punto “1 ora 08 minuti”), del seguente filmato .
-Considerando inoltre che per rintracciare la immagine della fenditura, in ritorno dalla riflessione dello specchio, è più comodo togliere quella fenditura da davanti al led, così da poter più agevolmente cercare il più ben visibile “pallino” luminoso del riflesso del led, non più nascosto dalla fenditura;
-Ed inoltre, anzichè usare un piccolo schermo traslucido come si vede nel filmato, è più comodo usare un semplice foglio di cartoncino da brandeggiare per rintracciare il riflesso, e completare l’allineamento del tester, portando quel dischetto luminoso del led, esattamente sulla lama del tester. FINE DELLA NOTA.
Se ora spostiamo la nostra testa indietro di una trentina di centimetri, e mettiamo una lente qualunque nella posizione dove prima avevamo l’occhio, vedremo la fenditura comparire sul vetro della lente.


La immagine della fenditura e alla sua destra, quella della lama che deve essere regolata esattamente parallela ad essa
Spostiamo allora in avanti la lama (cioè verso sinistra) in modo da farla comparire a destra della fenditura e portiamola avanti fino ad arrivare al bordo di essa.
Ora regoliamo l’orientamento della lama in modo che fenditura e lama siano parallele.
Avanzando la lama verifichiamo che la fenditura si estingua da cima a fondo nello stesso istante.
Notare che quando gli avanzamenti della lama sono così minuscoli da fare (cosa che succede anche nelle normali rilevazioni col tester) è molto più comodo non utilizzare la sua vite di regolazione, ma premere con due dita sulla base del supporto della lama, che con la sua leggerissima flessione elastica assolverà al compito desiderato.
ILLUMINAZIONE DELL’AMBIENTE DEL TEST
Predisponiamo la più conveniente illuminazione dell’ambiente per permettere all’occhio il minimo affaticamento e la massima sensibilità al contrasto, creando semioscurità in modo simile a quando si guarda la TV. Una lampada da testa, a luce rossa (o comunque a luce non tanto potente da infastidire l’occhio) ci permetterà di leggere bene sul micrometro di spostamento avanti-indietro del carrello, i valori dei tiraggi da registrare sul taccuino.
MISURAZIONE DEL RAGGIO DI CURVATURA E DELLA FOCALE DELLO SPECCHIO IN ESAME
Se dopo aver verificato il parallelismo fenditura-lama, inseriamo completamente quast’ultima nel cono di luce, vedremo la sua immagine proiettata sul lato della lama opposto allo specchio, potremo così manovrare il carrello del tester avanti o indietro in modo da migliorare il fuoco di tale immagine.
Raggiunto il punto di migliore fuoco occorre farsi aiutare da qualcuno a misurare con precisione al millimetro senza muovere alcun componente del setup installato, la distanza fra centro specchio e lama, ed anche la distanza fra fenditura e centro specchio. La media aritmetica della somma dei due valori è il raggio di curvatura dello specchio, che è il doppio della sua distanza focale.
Ma c’è un altro modo più preciso di trovare la lunghezza focale dello specchio, ed è quello di cercare la “tinta piatta” cioè il centro di curvatura della sua zona 1, che appare nella finestra centrale della maschera di Couder, iniziando di fatto la prima tornata di rilevazioni dei tiraggi delle zone. Cioè la prima sessione del test di Foucault.
La zona 1 è quella centrale dello specchio,ed è la più critica e impegnativa da misurare, come già anticipato nell’articolo dal titolo “TEST DI FOUCAULT A COSA SERVE E COME FUNZIONA”
E’ Critica perché è il luogo di partenza cui si riferiranno tutte le nostre misure relative da zona a zona, ed è quindi la più importante perché sbagliando quella, ci porteremo dietro l’errore su tutte le altre zone.
E’ Impegnativa perché è la più ampia ma è pure la meno deformata, e quindi richiede il maggior spostamento longitudinalmente il carrello del tester rispetto alle altre zone che saranno esaminate, ma il grave è che in tale grande spostamento pare sempre che sull’ombra visibile cambi poco o nulla, a causa della poca deformazione della zona.
Ciò quindi rende veramente difficile individuare, in quelle tonalità di grigio apparentemente sempre uguali, quale sia la famosa “tinta piatta” che individua esattamente il fuoco della zona.
Ogni operatore che incappa in quell’errore, impara a sue spese e si crea delle sue regole personali per trovare con certezza l’esatto fuoco.
La mia regola è la seguente:
- Spostare longitudinalmente il SOLO carrello del tester verso lo specchio (operando con la sua vite di regolazione longitudinale sull’asse ottico dello specchio) in una zona francamente intrafocale (cioè più vicina allo specchio rispetto al cetro di curvatura atteso), e introdurre la lama (operando con la sua vite di regolazione ortogonale) in modo tale che essa raggiunga il centro dello specchio, e annotare il tiraggio longitudinale di quel punto di partenza, letto sul micrometro di misura degli spostamenti avanti e indietro del carrello del tester. Con un tester “standard”, (cioè che introduce la lama da destra verso sinistra, vista dall’operatore che sta dietro al tester), l’ombra intrafocale vista sullo specchio raggiungerà il suo centro provenendo da destra: Supponiamo di leggere in quel punto il valore 55.96mm.
- Lasciare la lama in quella posizione e indietreggiare solo col carrello longitudinale allontatandoci dallo specchio finchè non si renda visibile l’ombra della lama raggiungere la stessa posizione specularmente simmetrica rispetto alla prima (cioè man mano che ci si allontana dallo specchio, l’ombra della lama la si vedrà arrivare nello stesso punto, ma proveniente da sinistra verso destra), e annotare il tiraggio di quel punto di arrivo extrafocale: Siccome il nostro tester è stato costruito nel modo “standard”, che oltre a prevedere l’introduzione della lama da destra verso sinistra, prevede l’aumento delle letture del micrometro con l’allontanamento del carrello dallo specchio, Supponiamo di leggere in quel punto 62.20mm.
Per differenza dei due valori (62.20-55.96=6.24mm) si trova la distanza di tiraggio che va dalla posizione iniziale intrafocale fino alla omologa posizione finale extrafocale. Dividendola per due troviamo (6.24/2=)3.12mm che sommati alla distanza della posizione iniziale 55.96 fornisce (55.96+3.12=) 59.08, che è la misura in cui spostare il carrello del tester.
Se tutto è andato liscio, quella posizione del carrello a distanza 59.08mm è la posizione del centro di curvatura della zona 1, e potremo verificarla guardando l’ombra mentre estrarremo e reinseriremo la lama trovando la presenza della “tinta piatta” data dal chiudersi dell’ombra grigia in modo concentrico e uniforme, senza mostrare provenienze di essa nè da destra nè da sinistra.
Aiutati da qualcuno misuriamo la distanza centro specchio – lama, la sommiamo alla distanza centro specchio fenditura, e dividiamo per due, trovando 2400 mm di Raggio R di curvatura, e con questo valore R correggiamo i valori di hm 2 /R nelle caselle delle zone sul nostro taccuino.
Trovata la lunghezza focale dello specchio (corrispondente a R/2) non dimentichiamo di trascrivere sul nostro taccuino, il valore del tiraggio rilevato per la zona n°1 del nostro 200F6 , che leggiamo essere 30.89mm. Non muoviamo il tester perchè continueremo da quella posizione la ricerca del centro di curvatura nelle altre tre zone via via più periferiche dello specchio.
TEST DI FOUCAULT: Esempi di ombre che si presentano all’operatore.
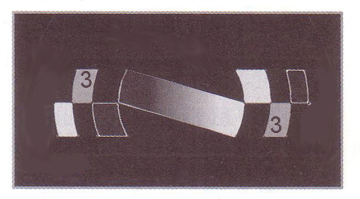
L’osservazione delle tinte piatte nella varie zone, si presenterebbe orientativamente come nelle seguenti 4 figure, in cui il numero all’interno della finestra, indica la sua tinta piatta.
Nota 1:
Ad esempio: Nella figura di zona 1 (zona virtualmente immaginabile come composta anch’essa da due finestre, una a destra ed una a sinistra del centro specchio), si nota che le due parti destra e sinistra si trovano in uniforme “tinta piatta”, e le ombre sono tutte nelle zone alla sua destra della. Cioè in esse ci troviamo in intrafocale, ovvero PRIMA del fuoco corrispondente a quelle zone periferiche (che infatti si tovano sbilanciate in grigio un poco diverso dalla tinta piatta, per la zona 2), ma siamo anche molto più intrafocali delle finestre delle zone 3 e 4, che pertanto al momento si presentano ancora in grigio molto scuro a destra e bianche a sinistra.
Nota 2:
Guardiamo la finestra centrale (zona 1) nelle figure successive alla prima, e la vediamo scurirsi sempre più, da sinistra verso destra man mano che controlliamo zone via via più periferiche. Il che indica chiaramente che in quel momento la zona 1 si trova già in evidente posizione extrafocale rispetto al punto attuale delle misurazioni. E si troveranno in uniforme tinta piatta, via via le coppie di finestre delle altre zone.



ESEGUIAMO QUINDI REALMENTE IL TEST
sullo specchio 200F6, con la ricerca delle tinte piatte di tutte le quattro zone, partendo dalla zona 1 in allontanamento dallo specchio, fino alla zona 4, con l’annotazione dei loro tiraggi sul taccuino.
- Una volta rilevate le zone 1,2,3,4, ci allontaniamo ancora un poco a vuoto per invertire poi il senso di rilevazione, e tornare indietro verso lo specchio, per una seconda serie di rilevazioni, delle zone 4,3,2,1.
- Ritornati nuovamente alla zona 1, avanziamo ancora un poco a vuoto per invertire ancora una volta il senso della rilevazione per una terza serie di dati, sulle zone 1,2,3,4 e passando un poco oltre.
- Ed infine invertiamo l’ultima volta per registrare l’ultima serie di dati delle zone 4,3,2,1.
Alla fine disporremo delle seguenti quattro serie di valori da mediare:
| Zone | Z1 | Z2 | Z3 | Z4 |
| Andata 1 | 30.89 | 31.39 | 31.74 | 31.9 |
| Ritorno 1 | 31 | 31.43 | 31.86 | 32 |
| Andata 2 | 31.2 | 31.52 | 31.82 | 32.11 |
| Ritorno 2 | 30.91 | 31.68 | 31.8 | 31.99 |
| Media | 31 | 31.5 | 31.8 | 32 |
Valori che utilizzeremo per la valutazione della superficie, che avevamo già registrati sul nostro taccuino durante e rilevazioni, come nella immagine seguente, nel riquadro in colore rosso.

La media dei valori delle quattro serie, si fa perché “ripara” gli errori commessi nella valutazione di un non esperto, aumentando grandemente l’affidabilità del calcolo che si eseguirà con essi. Tuttavia l’operatore esperto potrebbe tranquillamente farne a meno, o ridurla a una sola andata e ritorno.
Tornando ai nostri numeri:
Noi disponevamo già prima, dei valori di hm 2 /R che rappresentano l’aberrazione longitudinale della perfetta parabola di riferimento con focale 1200 e Raggio 2400mm, la quale con quei valori passerebbe esattamente nei centri delle finestre della nostra maschera di Couder: Valori di aberrazione che erano i seguenti.
Per la perfetta parabola di riferimento:
| Zona | 1 | 2 | 3 | 4 |
| Aberrazione | 0.14 | 1.08 | 2.28 | 3.46 |
(NOTA: Vale la pena di ricordare che in ottica si chiamano aberrazioni, le quantità delle”deformazioni” della sfera originale che realizzano la parabola desiderata. Normalmente, nel comune parlare, il termine “aberrazione” e dispregiativo. Ma in ottica esse sono le qualità positive che devono essere impresse nel vetro della sfera originale per ottenere la parabola desiderata).
Ed ora abbiamo appena trovato dei nostri di valori medi di “tiraggio” o aberrazioni ancora “grezze”, 31 ; 31.5 ; 31.8 ; 32 , perchè differiscono dai valori di riferimento 0.14 ; 1.08 ; 2.28 ; 3.46 , perché ai nostri è sommata una costante ignota, dovuta alla lettura della scala sul nostro micrometro di misura, che non poteva in alcun modo essere sincronizzato con i valori di calcolo della aberrazione teorica.
Quindi dovremo trovare quella costante per poterla sottrarre alle nostre misure per “portarle più vicine” possibile ai valori di riferimento in modo da rendere il confronto con esse più agevole ed evidente.
PAUSA PER UN RAGIONAMENTO INTERESSANTE:
Siccome in genere è conveniente (per il minor vetro da grattare), parabolizzare dal 70% del diametro, e dato che il raggio dello specchio noi lo chiamiamo tecnicamente hm, nel nostro caso deduciamo che il raggio appartenente al diametro 140mm cade nella zona 3 della nostra maschera, che ha hm = 74.
Imponendo quel punto di contatto, in pratica assumiamo che la zona 3 sia perfetta (cioè abbia differenza aberrazione zero, cioè coincida con la parabola di riferimento). E questo ci permetterà di vedere come e di quanto, le altre zone si allontanano rispetto ai valori della perfetta parabola di riferimento.
(notare che potremmo benissimo e lecitamente fare la stessa cosa imponendo come zona di contatto e riferimento “zero”, una qualsiasi delle altre zone dello specchio. Ma ciò in genere non conviene mai per troppo lavoro conseguente…a meno di casi particolari in cui si vi possa recuperare un errore maldestramente commesso, altrimenti difficile da eliminare).
FINE DEL RAGIONAMENTO
APPLICHIAMO QUINDI I NOSTRI PROPOSITI
Per “spostare” in modo matematico la nostra zona 3 a contatto con la zona 3 della parabola perfetta, dobbiamo sottrarre al nostro tiraggio misurato in zona 3, il valore della sua perfetta aberrazione di riferimento hm 2 /R , che è 2.28, e troviamo un valore che rappresenta la costante di spostamento da sottrarre ANCHE a ciascuna delle altre nostre tre zone, perchè solo così realizzeremo la perfetta simulazione della sovrapposizione con contatto fisico nella zona 3, della nostra parabola, con quella di riferimento.
Troviamo la costante:
| Tiraggio Z3 | 31.8 | – |
| [hm 2 /R] Z3 | 2.28 | = |
| Costante | 29.52 |
E la sottraiamo da tutte le altre zone:
| Zona | 1 | 2 | 3 | 4 |
| Tiraggio | 31- | 31.5- | 31.8 | 32- |
| Costante | 29.52 | 29.52 | 29.52 | 29.52 |
| Valori residui | 1.48 | 1.98 | 2.28 | 2.48 |
A questi valori sottrarremo ancora l’aberrazione della parabola di riferimento, e il risultato sarà l’errore che affligge la nostra parabola, espresso in pendenza percentuale, ovvero in mm pendenza che la superficie avrebbe ogni 100mm di larghezza della zona.
| Zona | 1 | 2 | 3 | 4 |
| Misure ridotte | 1.48- | 1.98- | 2.28- | 2.48- |
| hm 2 /R | 0.14= | 1.08= | 2.28= | 3.46= |
| Pendenze % | 1.34 | 0.9 | 0 | -0.98 |
| anche dette “Misure ridotte” |
Il tutto come già rilevato nella seguente immagine del taccuino, nel riquadro rosso.

Vediamo quindi che la differenza di forma fra la nostra parabola attuale e quella di riferimento è data in questo caso, da due valori di pendenza positivi in zona 1 e 2; un valore di pendenza zero in zona 3 (che è il punto di contatto che noi abbiamo imposto identico alla parabola di riferimento), e un valore negativo in zona periferica 4
I VALORI POSITIVI Indicano di quanti millimetri il raggio di curvatura della superficie di quella zona è troppo grande (beninteso in riferimento al valore della zona 3 che noi abbiamo scelto come coincidente con la parabola teorica.
GRAFICO: Per i valori positivi (raggio troppo grande) il grafico che esprime quel valore come pendenza percentuale SCENDE .
I VALORI NEGATIVI Indicano quindi un raggio di curvatura troppo piccolo in quella zona
GRAFICO: Per valori negativi (raggio troppo piccolo) il grafico espresso in percentuale SALE.
(SUGGERIMENTO PRATICO: Per memorizzare l’apparente controsenso che un valore positivo scenda invece di salire, fa comodo pensare che per noi grattatori di vetro , che lavoriamo per asportazione di vetro, quella parte di specchio è alta e può, e deve essere “abbassata”. E viceversa quella che sale, perchè è già troppo in basso, e non si può rialzare se non abbassando tutte le altre zone).
Per disegnare il grafico delle pendenze percentuali, partiremo dalla linea verticale sinistra della colonna che rappresenta la zona 1 nel nostro taccuino, e tracceremo una linea “di costruzione” orizzontale (nel grafico è tratteggiata) lunga 100mm, all’ estremo della quale (siccome la zona 1 è positiva , e la pendenza scende) ne abbasseremo una verticale lunga 1.34mm, cioè quanto è la misura di aberrazione ridotta della zona 1.
Collegheremo poi questo vertice con l’origine disegnando una linea (che è la ipotenusa di un triangolo rettangolo) che ha pendenza 1.34% e non la estenderemo per 100mm ma la termineremo alla intersezione della linea verticale laterale destra della stessa colonna di zona 1, perché non è la lunghezza che ci interessa , ma solo la vista della inclinazione e del suo senso.
Partiremo poi a disegnare la pendenza della zona 2, da dove è terminata la pendenza 1, e tracceremo anche qui una orizzontale “di costruzione” lunga 100mm, dalla quale dirigeremo in verticale verso il basso una linea lunga 0.9mm, e collegheremo le due linee verticali laterali che delimitano la colonna di zona 2, con una linea non importa quanto lunga ma avente quella pendenza.
Partiremo ancora dal termine destro della linea di pendenza della zona 2 per tracciare una orizzontale (con pendenza zero) imposta da noi artificiosamente in zona 3.
Ed infine dal termine destro della linea orizzontale della pendenza zero di zona 3, tracceremo la solita linea di costruzione lunga 100mm dall’ estremo della quale innalzeremo (perché il valore è negativo e la pendenza sale) una linea lunga 0.98mm, unendo il vertice della quale all’origine sul confine della zona precedente, avremo la pendenza a salire della periferia dello specchio..
E COL GRAFICO TRACCIATO SIAMO GIUNTI AD EVIDENZIARE IL RISULTATO .
Infatti il grafico ci dice che il nostro specchio ha un centro ed un bordo rilevati, e quindi la prossima correzione da attuare sarà quella di abbassare il centro.
Conviene infatti sempre lasciare per ultime le correzioni del bordo, che è il luogo più critico di tutta la lavorazione. Infatti lavorando per abrasione possiamo solo asportare vetro, e non possiamo aggiungerne qualora avessimo esagerato nella asportazione al bordo specchio dove la tolleranza è la più ristretta.
In quel caso, per recuperare l’errore dovremmo cancellare il lavoro fatto, tornando verso la sfera con un certo numero di corse di abrasione 1/3 C.O.C. (Vedi articolo che le descrive in questo stesso blog), per riprendere una nuova azione di parabolizzazione. Oppure in alternativa potremo provare a prendere una diversa zona di contatto con la parabola di riferimento, per vedere se non si presentano altre zone basse. (Ma spesso è la quantità di lavoro di abrasione che ne conseguirebbe, a rendere non conveniente questa possibilità).
A PROPOSITO DEL GRAFICO DISEGNATO IN MODO MANUALE:
Quello di questa immagine, che ho tracciato a fondo pagina, è in scala millimetrica, e pertanto è poco istruttivo perchè difficilmente leggibile anche se si ingrandisce con un click, rispetto allo stesso grafico che ho riprodotto in scala diversa e più utile, al termine di questo articolo . Tuttavia sono tutti e due veritieri, e come andamento identico al grafico che nella prossima puntata vedremo per questo stesso test n°1, realizzato con un software fra i tanti per il test Foucault.
Per la leggibilità di questo ed anche di altri grafici eseguiti in modo manuale, c’è da dire che al grattatore di vetro (per poter pensare a quale correzione mettere in atto per migliorare la parabola) basta vedere a colpo d’occhio due sole informazioni relative al “dove” sono i punti in cui intervenire, e al “quanto” ampio è il difetto:
1) per avere una idea della gravità degli errori della superficie, leggibili come distanza delle punte alte e basse delle zone rispetto allo zero della zona di riferimento.
2) per vedere l’orientamento delle pendenze (perchè le zone alte si possono abbassare per abrasione, ma le zone già troppo basse non si possono alzare… se non abbassando tutto il resto, cioè tornando verso la sfera con corse 1/3 D c.o.c.).
3) Per quanto riguarda il “quanto” correggere quelle zone alte: Al grattavetro è indicativo il numero che esprime la percentuale di pendenza, che suggerisce la pesantezza dell’azione correttiva.
Quindi alla luce di un utilizzo pratico, il disegno di un grafico in scala millimetrica è poco interessante perchè poco leggibile, e per una migliore visibilità della entità proporzionale dei difetti delle singole zone rispetto alle altre, conviene amplificare le scale orizzontale e verticale, in modo diverso e arbitrario.
Come nell’esempio della immagine seguente, dove la scala orizzontale della larghezza delle zone è di 10 quadretti della carta, anzichè di 100mm; Mentre la scala verticale delle pendenze è pure espressa in quadretti anzichè in millimetri , ma per migliorarne il confronto visuale, è tre volte maggiore del valore millimetrico, ossia ad esempio la zona 1, che ha pendenza 1,34mm, diventa sul grafico una pendenza di (1,34×3)=4,02 quadretti della carta del foglio di taccuino.
In questo modo si esagera lecitamente l’inclinazione delle pendenze con la stessa scala. Il che risulta più efficace per la comprensione immediata ” a colpo d’occhio” delle entità dei difetti delle zone, e ottima guida per la previsione del lavoro di ritocco da mettere in pratica nel prosieguo della lavorazione.

Segue con l’articolo: “200F6 studio sul 1° test di Foucault”

