E’ utile a questo punto, un richiamo sulle tecniche di lavorazione con gli utensili a sub-diametro, in particolare su come sia possibile incrementare la curvatura di una o più zone.
Riprendiamo quindi il concetto secondo il quale durante le passate con il sub-diametro, le zone esterne aumentano la loro curvatura mentre quelle interne la diminuiscono, il che equivale a dire che durante le passate generiamo un “solco” sulla superficie, dove il settore centrale della zona lavorata è più profondo rispetto al resto della superficie non lavorata.
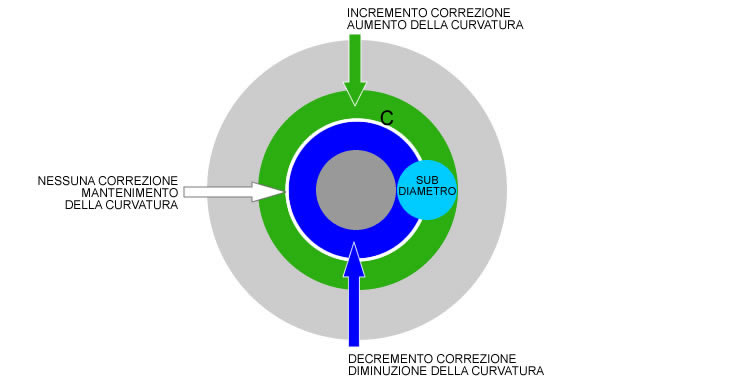
Fig. 1 – Azione del sub-diametro sulla curvatura superficiale
In teoria ( ma non in pratica ) la sola applicazione di questa tecnica è sufficiente per raggiungere il risultato voluto. vediamo come:
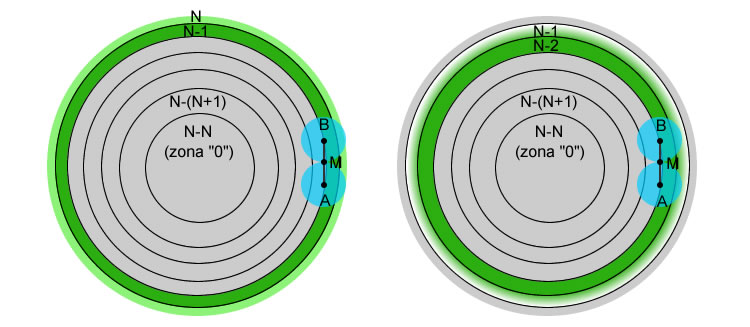
Fig. 2 – Sequenza degli aumenti della curvatura in zone adiacenti.
Assumiamo N come il numero totale delle zone in cui divideremo virtualmente il nostro specchio . Avremo quindi la nostra successione di zone ( settori circolari di ampiezza predefinita ) partendo dal bordo verso il centro specchio: N, N-1, N-2, ….. , N-N.
La nostra ipotesi di partenza ci dice che sfera e parabola sono coincidenti nel bordo, ma dato che nei test non avremo mai modo di misurare la curvatura nel bordo, nulla ci vieta di “spostare” questo punto di tangenza ( che ricordiamo può essere scelto in modo arbitrario in un qualunque punto della sezione sferica di partenza ) al centro della zona più periferica ( N ) , proprio nel punto dove viene effettuata la misura.
Avremo quindi che il centro dell’ultima zona è per definizione “corretto”, essendo tangente sia alla sfera che al profilo parabolico di progetto e pertanto non dovrà essere lavorato, inizieremo quindi a scavare il centro della successiva zona N-1 fino a quando anch’esso non sarà tangente al profilo parabolico voluto.
Per fare questo dobbiamo rendere la zona N-1 ed il suo centro più profondo di quello della zona N rispetto alla sfera di partenza, in altre parole dobbiamo aumentare la curvatura della sfera iniziale spostandoci da N-1 a N.
Applicando quindi la citata tecnica del sub-diametro, prepareremo un utensile il cui raggio sia leggermente superiore alla distanza dei centri di due zone successive , posizioneremo il centro dell’utensile sul bordo interno della zona N-1 ed effettueremo piccole corse di va e vieni con andamento circolare tutto intorno alla zona. Il risultato sarà che avremo aumentato la curvatura esattamente tra la zona N-1 ed N. Effettueremo la misura di questo incremento con un test adeguato, limitandoci a misurare solo il “tiraggio” di queste due zone, e ripeteremo le sessioni con il sub-diametro fino a quando la misura del tiraggio non sarà coincidente con quella della simulazione ( calcolata matematicamente o via software ) della nostra parabola finale .
A questo punto avremo due zone corrette rispetto alla parabola finale. Passeremo quindi alla zona successiva N-2 e ripeteremo la stessa procedura di “scavo” e raccordo tra la N-1 e la N-2 fino a portare anche questo tiraggio al valore corretto.
Applicheremo la procedura in successione fino all’ultima zona N-N ( il centro dello specchio o “zona 0” ) per far si che l’ultima zona “utile” , la N-(N+1) , ovvero la prima zona centrale , completi la configurazione ed il raccordo della parabola.
DENTRO LA “TROMBA DI TOLLERANZA”
la generazione della parabola come approfondimento crescente di zone consecutive, può essere anche vista come successione di zone portate “in tolleranza” nel grafico Millies-Lacroix. Per fare questo dobbiamo però ricorrere ad un piccolo “trucco” che ci aiuterà nella immediata visualizzazione di quello che andremo a fare.
La nostra sfera di partenza con identici raggi di curvatura delle zone ( tiraggio=0 ) inserita nel grafico ML di un ipotetico specchio 300 mm F4 parabolico, avrebbe una rappresentazione simile a questa:
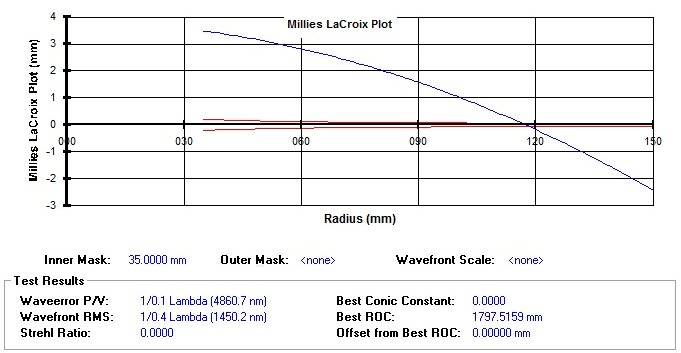
Fig. 3 – Grafico Millies-Lacroix per una superficie sferica ( la scala è alterata per una migliore visualizzazione )
Applichiamo ora la nostra prima ipotesi, quella cioè di tangenza nel bordo tra sfera e parabola,( anziché al raggio 115 mm come rappresentato in figura) , che equivale a traslare la curva verso l’alto fino a far cadere il centro di curvatura del raggio 150 mm al centro della tromba di tolleranza:
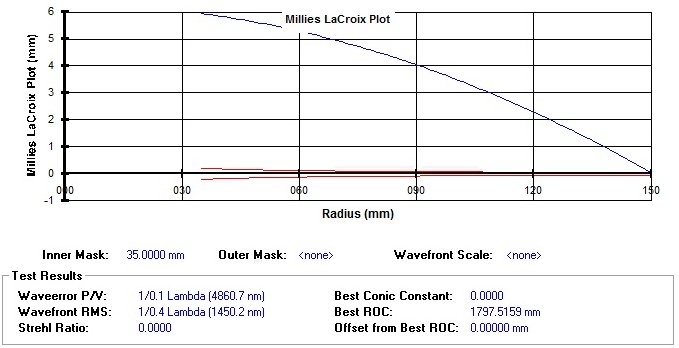
Fig. 4 – Grafico Millies-Lacroix per una superficie sferica tangente al bordo con il paraboloide ideale ( la scala è alterata per una migliore visualizzazione )
la traslazione ( il “trucco” ) che abbiamo appena fatto sul Grafico Ml corrisponde quello che abbiamo scelto di fare al punto B della prima parte dell’articolo:
B – “Accorciamo” le riflessioni centrali: equivale a dire che partendo dal bordo e spostandoci verso il centro aumenteremo gradatamente la curvatura dello specchio in modo che le riflessioni delle zone centrali convergano più vicino, quel tanto che basta per farle coincidere con quelle periferiche.
Guardando il grafico impostato in questo modo, è abbastanza intuitivo che, per portare la sfera verso la parabola, tutta la curva dovrà entrare in tolleranza, dobbiamo perciò approfondire la superficie (“tirare giù” la curva ) in maniera crescente a partire dal bordo verso il centro
Supponiamo di aver calcolato i valori esatti dei centri di curvatura della nostra parabola ideale e di lavorare lo specchio secondo la procedura descritta, portando dapprima all’esatto raggio di curvatura la zona N-1 ( in questo esempio N=5 ) e successivamente tutte le altre. Ecco cosa dovremmo aspettarci nel grafico ML calcolato con il test di foucault, ovvero la sequenza delle correzioni zona dopo zona :
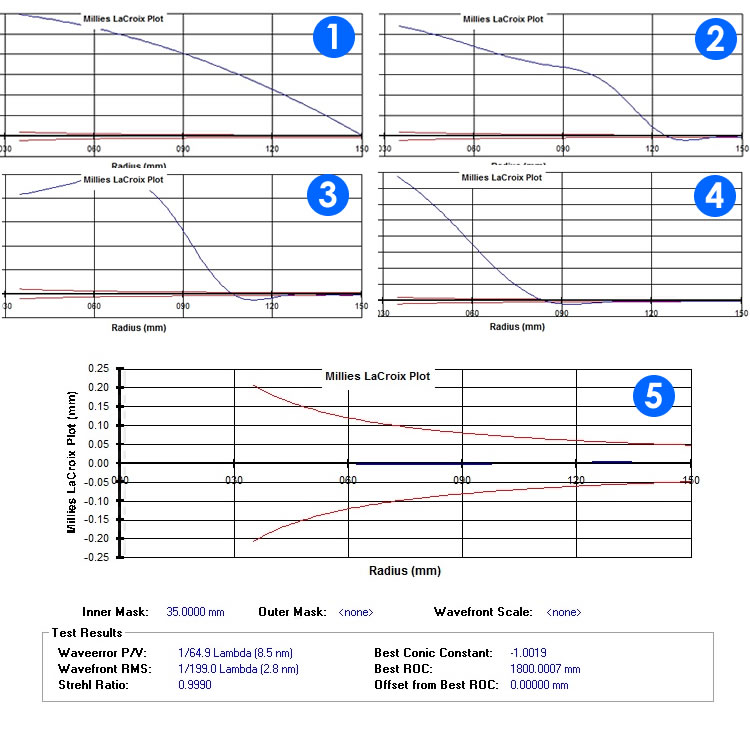
Fig. 5 – Successione degli approfondimenti zonali.
DALLA TEORIA ALLA PRATICA
Come accennato, nella realizzazione pratica le cose sono meno immediate, intervengono infatti diversi elementi che sconsigliano un approccio così diretto, occorrerà trovare preventivamente delle soluzioni alle seguenti problematiche:
- per focali corte il numero delle zone da esaminare deve essere ragionevolmente elevato, maggiore è il numero delle zone minore è l’estensione dell’utensile che permette di lavorare solo due zone adiacenti senza interferire con le altre, con intuibili incrementi dei tempi di lavorazione.
- Aumentando la curvatura della zona esterna diminuisce di conseguenza quella della zona interna la quale dovrà essere successivamente approfondita sia del valore rispetto alla sfera che del valore aggiuntivo di decremento della curvatura appena generato.
- minore è l’estensione dell’utensile, maggiore è la probabilità di generare errori superficiali locali di difficile correzione, i “piccoli” sub-diametro andrebbero utilizzati con parsimonia , per piccole correzioni e con una buona esperienza di utilizzo in configurazioni meno “estreme”.
- Difficilmente si arriverà alla misura esatta del tiraggio di due zone agendo in un solo senso, quello cioè del solo incremento della curvatura. E’ probabile che avvicinandosi alla figura ideale si ecceda ( anche se di pochissimo ) nella lavorazione e sia necessario “tornare indietro” agendo cioè nel senso opposto di decremento della curvatura, con diretta ed inevitabile conseguenza di modifica della forma anche sulle zone adiacenti.
- Questa procedura non permette un controllo globale della superficie durante la costruzione della figura, specialmente con i test complementari come il Ronchi, è basata sulla “fiducia” che stiamo lavorando bene, ma la conferma potrà arrivare soltanto dopo aver completato la tutta parabola.
Questo ultimo punto può essere meglio evidenziato se simuliamo il grafico del Test di Ronchi corrispondente alle fasi di lavorazione zona dopo zona:

Fig. 6 – Simulazione del Test di Ronchi per la successione di approfondimento zonale.
Come si può vedere nella Fig.6 , questa metodologia pur mantenendo le buone premesse iniziali, non consente di valutare con immediatezza quanto la lavorazione sia sulla “stada giusta”, solo dopo aver portato tutte le zone a misura potremo valutare la correzione superficiale nella sua globalità.
Occorre quindi ottimizzare questa strategia durante tutto il lavoro di costruzione della figura, per rendere possibile il controllo della qualità della lavorazione durante ogni fase, eliminando o perlomeno riducendo al minimo le possibilità di errori locali o generali e che permetta comunque di individuarli con certezza e di intervenire “in sicurezza” qualora si presentassero.
E’ quello che cercheremo di scoprire nella terza parte.